エピトロコイド平行曲線の特異点

サイクロ減速機

平行曲線と特異点

エピトロコイド平行曲線のオフセット量を増やしていくと、元の曲線から大きく形が崩れる地点があります。
具体的には曲線が交差したりし始めます。
灰色の線がそれです。
f:id:woodenCaliper:20190313011127p:plain

この曲線にある尖点（尖がっている部分）を特異点と呼びます。
この特異点が発生しない平行曲線にしなければなりません。
特異点が発生するオフセット量は最小の曲率半径を超えたときに発生します。
(厳密な証明はしていないので間違っている可能性あり)

最小の曲率半径

曲率半径の計算式は、媒介変数表示の場合、

\begin{aligned} R &= \frac {\left( \left(\frac{dx}{d\theta_c}\right)^2 + \left(\frac{dy}{d\theta_c}\right)^2 \right)^\frac{3}{2}} {\frac{dx}{d\theta_c} \frac{d^2y}{d\theta_c^2} - \frac{dy}{d\theta_c} \frac{d^2x}{d\theta_c^2}} &= \frac { \left( x^{\prime2} + y^{\prime2} \right)^{\frac{3}{2}} } { x^{\prime} y^{\prime\prime} - y^{\prime} x^{\prime\prime} } \end{aligned}

最小の曲率半径を知りたいので、

\begin{aligned} \frac{dR}{d\theta_c} = 0 \end{aligned}

の時の \theta_cを求めればよいです。

\begin{aligned} \frac{dR}{d\theta_c} = \frac { 3 \left(x_a^{\prime2} + y_a^{\prime2}\right)^\frac{1}{2} \left(x_a^{\prime} x_a^{\prime\prime} + y_a^{\prime} y_a^{\prime\prime}\right) \left( x_a^{\prime} y_a^{\prime\prime} - y_a^{\prime} x_a^{\prime\prime}\right) - \left(x_a^{\prime2} + y_a^{\prime2}\right)^\frac{3}{2} \left( x_a^{\prime} y_a^{\prime\prime\prime} - y_a^{\prime} x_a^{\prime\prime\prime} \right) } {\left( x_a^{\prime} y_a^{\prime\prime} - y_a^{\prime} x_a^{\prime\prime}\right)^{2}} \end{aligned}

エピトロコイド曲線の式は

\begin{aligned} x_a &= (r_c+r_m) cos\theta_c - r_d cos \left(\frac{r_c+r_m}{r_m} \theta_c \right) \end{aligned}
\begin{aligned} y_a &= (r_c+r_m) sin\theta_c - r_d sin \left(\frac{r_c+r_m}{r_m} \theta_c \right) \end{aligned}

なので、 R^{\prime}=0の時の\theta_cを頑張って解くと、

\begin{aligned} \theta_c =　[& 0.0,　 \frac{r_m}{r_c}\pi, 　 \pm \frac{r_m}{r_c} cos^{-1}{\left (\frac{r_d^{2} + r_m^{2}}{2r_d r_m} \right )}, \\ &\pm \frac{r_m}{r_c} cos^{-1}{\left (\frac{2 r_c r_d^{2} - r_c r_m^{2} + r_d^{2} r_m + r_m^{3}}{r_d r_m \left(r_c + 2 r_m\right)} \right )} ] \end{aligned}

となります。6つ解がありますが、3つ目の解は、

\begin{aligned} \frac{r_d^{2} + r_m^{2}}{2r_d r_m} &= \frac{(r_d-r_m)^{2}+2r_d r_m}{2r_d r_m} &= \frac{(r_d-r_m)^{2}}{2r_d r_m} + 1 &>1 \end{aligned}

となるので、常に虚数解になります。
そのため実数解は、

\begin{aligned} \theta_c =　[& 0.0,　 \frac{r_m}{r_c}\pi, 　 \pm \frac{r_m}{r_c} cos^{-1}{\left (\frac{2 r_c r_d^{2} - r_c r_m^{2} + r_d^{2} r_m + r_m^{3}}{r_d r_m \left(r_c + 2 r_m\right)} \right )} ] \end{aligned}

となります。
0の点は歯底の部分にあたり、 \frac{r_m}{r_c}\piの点は歯先にあたります。

確認その１

パラメータを
r_c=36,　r_m=9,　r_d=3
に設定します。

一歯分の曲率半径とその微分のグラフはこんな感じです。

f:id:woodenCaliper:20190328221915p:plainf:id:woodenCaliper:20190328221925p:plain
左：曲率半径、右：曲率半径の微分

R^{\prime}=0の時の\theta_cは、 \theta_c=[0.0, 　\frac{\pi}{4},　-0.785398163397448,　0.785398163397448 ]
この\theta_cの時の曲率Rは、
R=[−30.0,30.0,30.0,30.0 ]

なので最大のオフセット量は30になります。
このときのエピトロコイド曲線とエピトロコイド平行曲線は下図になります。
f:id:woodenCaliper:20190328223117p:plain

次に、本当に30がオフセット量の限界なのかを簡単に確認します。
曲線に特異点がある場合、曲線のどこかに
\frac{dx}{d\theta_c} = \frac{dy}{d\theta_c} = 0
が存在しているはずです。

f:id:woodenCaliper:20190328225351p:plainf:id:woodenCaliper:20190328225226p:plain
左:rd=29　右:rd=30

図を見ると、オフセット量に当たるrdが29の時は、 \frac{dx}{d\theta_c} = \frac{dy}{d\theta_c} = 0の点が無く、rd=30の時は存在することが分かります。

確認その２

パラメータを
r_c=36,　r_m=4,　r_d=3
に設定します。

一歯分の曲率半径とその微分のグラフはこんな感じです。

f:id:woodenCaliper:20190328230735p:plainf:id:woodenCaliper:20190328230748p:plain
左：曲率半径、右：曲率半径の微分

R^{\prime}=0の時の\theta_cは、 \theta_c=[0.0, 　\frac{\pi}{9},　-0.1377,　0.1377 ]
この\theta_cの時の曲率Rは、
R=[−0.3846,　14.41,　11.30,　11.30 ]

なので最大のオフセット量は11.30になります。
このときのエピトロコイド曲線とエピトロコイド平行曲線は下図になります。
f:id:woodenCaliper:20190328230640p:plain

次に、本当に11.30がオフセット量の限界なのかを簡単に確認します。
曲線に特異点がある場合、曲線のどこかに
\frac{dx}{d\theta_c} = \frac{dy}{d\theta_c} = 0
が存在しているはずです。

f:id:woodenCaliper:20190328231132p:plainf:id:woodenCaliper:20190328231352p:plain
左:rd=11　右:rd=11.30

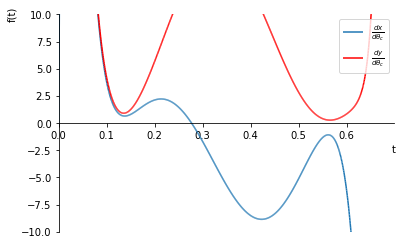
図を見ると、オフセット量に当たるrdが11の時は、 \frac{dx}{d\theta_c} = \frac{dy}{d\theta_c} = 0の点が無く、rd=11.50の時は存在することが分かります。

これらのように、曲率最小値を境に特異点のある無しが切り替わっていることが分かります。

これでサイクロ減速機の外ピンの直径の最大値を求めることができます。
スクリプトに組み込むことにします