2段サイクロ減速機の減速比の導出

サイクロ減速機 ハードウェア

以前、この記事で計算方法が分からないと言っていたのですが、分かったので記事にしました。

woodencaliper.hatenablog.com

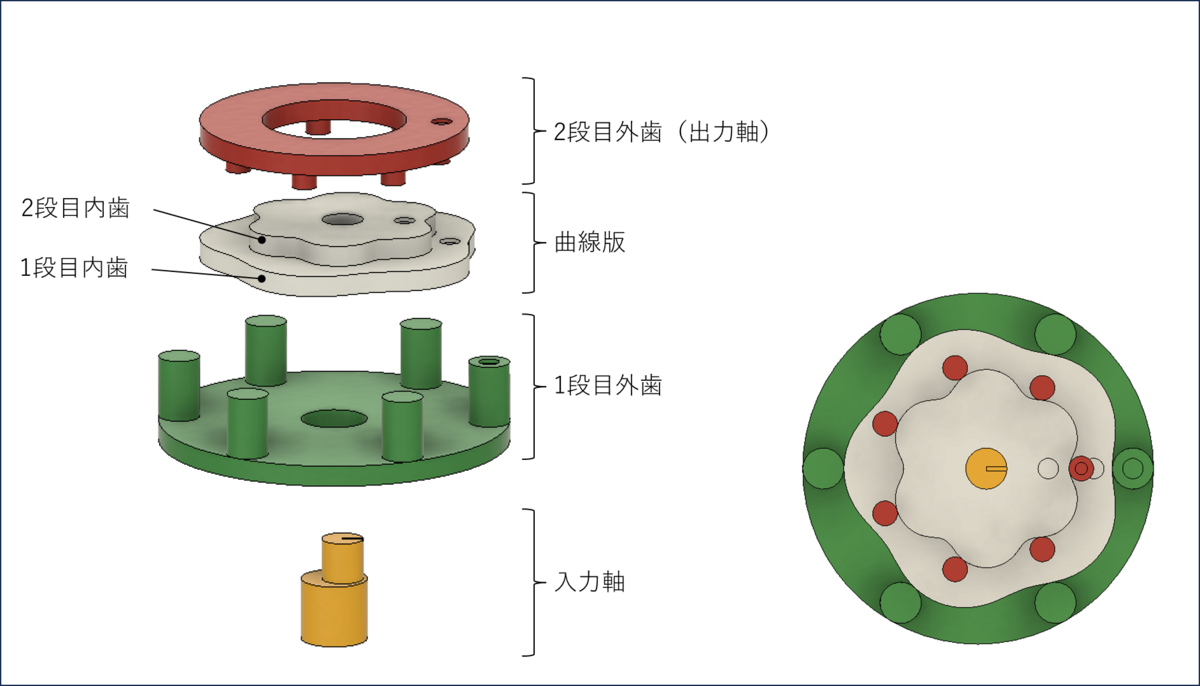
改めて説明すると、 下図のような入力軸、1段目外歯&内歯、2段目外歯&内歯、という構成になっている減速機の減速比の計算方法が分からないという話です。

結論

減速比は、

  • 1段目の内歯数 : n_{i1}
  • 1段目の外歯数 : n_{o1}
  • 2段目の内歯数 : n_{i2}
  • 2段目の外歯数 : n_{o2}

とすると、

{ \displaystyle =\frac{1}{n_{o2}} \left( \frac{-n_{i2} n_{i1}+n_{i2}n_{o1}+n_{i1}} {n_{i1}} \right) }

となり、

内歯と外歯の歯数差は1という条件を加えると、
{ \displaystyle n_{o1} = n_{i1}+1 \\ n_{o2} = n_{i2}+1 }
で、

{ \displaystyle \frac{n_{i1}-n_{i2}} {n_{i1} (n_{i1}+1) } }

となります。
つまり、1段目の内歯数と2段目の内歯数の差が1の時が最大の減速比となります。

導出

入力軸～2段目内歯までの減速

入力軸が1回転すると、
自転方向に { \displaystyle 1-\frac{n_{o1}}{n_{i1}} } 回転し、
公転方向に1回転する。

2段目内歯～2段目外歯の減速

サイクロ減速機の外歯と内歯の回転速度の関係

  • 内歯数 : n_{i}
  • 外歯数 : n_{o}
  • 内歯の自転角速度 : \omega_{iz}
  • 内歯の公転角速度 : \omega_{ik}
  • 外歯の自転角速度 : \omega_{oz}
  • 外歯の公転角速度 : \omega_{ok}

としたら、
速度比の関係は下記になる。

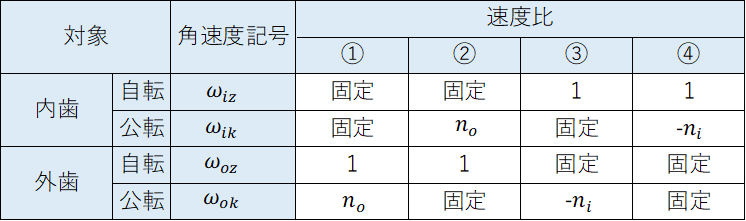
下記は内歯の自転と公転を固定した例

これらから各角速度の関係は

① { \displaystyle \omega_{oz} = n_o \omega_{ok} }

② { \displaystyle \omega_{oz} = n_o \omega_{ik} }

③ { \displaystyle \omega_{iz} = -n_i \omega_{ok} }

④ { \displaystyle \omega_{iz} = -n_i \omega_{ik} }

となる。

外歯の自転と内歯の自転公転の関係

①～④の式より

⑤ { \displaystyle \omega_{iz} = -\frac{n_i}{n_o} \omega_{oz} }

⑥ { \displaystyle \omega_{ik} = \frac{1}{n_o} \omega_{oz} }

となる。

トータル減速比

入力軸が1回転すると、1段目と2段目の内歯（曲線版）が、
自転方向に { \displaystyle 1-\frac{n_{o1}}{n_{i1}} } 回転し、
公転方向に1回転する。

2段目の内歯（曲線版）が、
自転方向に1回転すると、 { \displaystyle -\frac{n_{i2}}{n_{o2}} } だけ回転し、
公転方向に1回転すると、 { \displaystyle \frac{1}{n_{o2}} } 回転する。

つまり、
{ \displaystyle \left( 1-\frac{n_{o1}}{n_{i1}} \right) \left( -\frac{n_{i2}}{n_{o2}} \right) +\left( 1 \right) \left(\frac{1}{n_{o2}} \right) \\ }

{ \displaystyle =\frac{1}{n_{o2}} \left( \frac{-n_{i2} n_{i1}+n_{i2}n_{o1}+n_{i1}} {n_{i1}} \right) }
となる。

内歯と外歯の歯数差は1という条件を加えると、
{ \displaystyle n_{o1} = n_{i1}+1 \\ n_{o2} = n_{i2}+1 }
で
{ \displaystyle \frac{n_{i1}-n_{i2}} {n_{i1} (n_{i1}+1) } }
となる。

余談

軸から別軸に速度が伝わる際に起こる変換を行列で表すと、

  • 「モータ軸の回転→入力軸の自転公転」の変換行列　： \vec{A}
  • 「入力軸の自転公転→曲線板の自転公転」の変換行列： \vec{B}
  • 「曲線板の自転公転→出力軸の自転公転」の変換行列： \vec{C}

1行目を自転、2行目を公転として表すと

{ \displaystyle \begin{pmatrix} \omega_{o2z} \\ 0 \end{pmatrix} =\vec{C} \vec{B} \vec{A} \begin{pmatrix} \omega_m \\ 0 \end{pmatrix} }
{ \displaystyle \begin{pmatrix} \omega_{i2z} \\ 0 \end{pmatrix} = \begin{pmatrix} -\frac{n_{i2}}{n_{o2}} & \frac{1}{n_{o2}} \\ 0 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ 0 & -\frac{n_{i1}-n_{o1}}{n_{i1}} \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} \omega_m \\ 0 \end{pmatrix} }